Introduction to Simple Boosting Regression in Python

This post will consist of an introduction to simple boosting regression in Python. Boosting is a popular ensemble technique, and forms the basis to many of the most effective machine learning algorithms used in industry. For example, the XGBoost package routinely produces superior results in competitions and practical applications.

Table of Contents

Motivation: Why Boosting?

Like bagging and random forest, boosting involves combining multiple weak learner models, each of which performs poorly on their own. What makes boosting different is how these models are combined: instead of having weak learner runs in parallel, in boosting these models are run sequentially. In this way, each successive weak learner is able to adapt to the results of the previous models in the sequence. This procedure generally decreases bias.

Boosting arose out of a question posed in the paper by Kearns 1988 and Kearns and Valiant 1989: can a group of weak learner models be combined to yield a single effective learner (i.e. strong learner)? The paper by Robert Schapire 1990 found that the answer to this question is yes, and this work outlined the development of the first boosting algorithm.

Assumptions and Considerations

Some key points to keep in mind when using a boosting regressor:

Choice of hyperparameters is very important to obtain good results. Failure to do so will likely result in overfitting/underfitting
Assumptions of the weak learner, used to build the ensemble, should be considered
Outliers can cause problems if present in the data. Boosting regressors can place too much weight on these samples which will affect performance
As boosting is a sequential algorithm, it can be slow to train. This can affect the scalability of the model

Derivation of a Simple Boosting Regression Algorithm

Boosting involves the use of multiple weak learner models in sequence. The basic idea of the algorithm is as follows:

Provide some training data { $\bold{X},\bold{y}$ } to the first weak learner $f_1$ in the sequence. Fit the weak learner to these data
Obtain the predictions $\hat{\bold{y}}$ from the weak learner on the training data, and compute the residual $\bold{r}_1$
Replace the labels used when training $f_1$ with the computed residual, such that our training data is now { $\bold{X},\bold{r}_1$ }
Use our modified data { $\bold{X},\bold{r}_1$ } to train $f_2$
Repeat the previous steps for each of the weak learner models we have in the ensemble $f_1,f_2,\dotsf_n$

We can illustrate this procedure for a small boosting ensemble of $n=4$ :

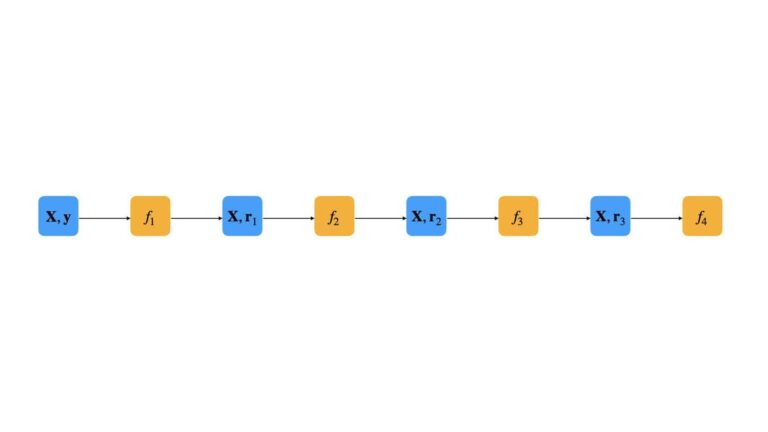
In this fashion, each successive weak learner is trained on the errors from the previous model. The net result is that the ensemble progressively improves as we move through the sequence.

But how are all these weak learners combined to yield a net result? Enter here the learning rate $\alpha$ . This is a hyperparameter to the boosting ensemble, and it controls the degree to which the output $\hat{\bold{y}}_i$ effects the calculation of the residual $\bold{r}_i$ . Normally, values of $\alpha$ range from 0.1 to 0.0001. The key here is to learn slowly, so as to avoid overfitting. The learning rate needs to be balanced with the other important hyperparameter here: the number of elements in the ensemble $n$ . Typically, $\alpha$ and $n$ need to be balanced off one another to obtain the best results.

We can now put this all together to yield the boosting algorithm for regression:

Initialise the ensemble $E(\bold{x}) = 0$ and the residuals $\bold{r} = \bold{y}$
Iterate through the i = 1…n models in the ensemble:
- Fit the weak learner $f_i$ to { $\bold{X},\bold{r}$ }
- Produce output $\hat{\bold{y}}$ from $f_i$ . Update the residuals using the learning rate: $\bold{r} = \bold{r} – \alpha\bold{\hat{y}}$
- Append the trained model to the ensemble: $E(\bold{x}) = E(\bold{x}) + \alpha f_i(\bold{x})$
Produce the trained boosted model: $E(\bold{x}) = \alpha\sum_{i=1}^{n}f_i(\bold{x})$

Implementation of Simple Boosting Regression in Python

Now let’s put what we’ve learned in the previous section to practice! First, it’s important to note that our boosting algorithm does not specify the form of $f_i$ . The only thing we know is that it is a weak learner. In practice, $f_i$ is almost always a decision tree with a limited number of splits. It is common to use trees with just 1 split: a decision stump:

Let’s begin by importing all the required packages:

## imports ##
import numpy as np
import pandas as pd
from typing import Dict, Any, List
from sklearn.base import clone
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_validate
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score,make_scorer

Model Implementation

I will encapsulate the algorithm outlined earlier in a single class, BoostingRegressor. Let’s now look into the details of the implementation:

## boosting regressor ##
class BoostingRegressor(object):
    #initializer
    def __init__(self, weak_learner : Any, n_elements : int = 100, learning_rate : float = 0.01) -> None:
        self.weak_learner  = weak_learner
        self.n_elements    = n_elements
        self.learning_rate = learning_rate
        self.f             = []
        self.residuals     = []
        
    #destructor
    def __del__(self) -> None:
        del self.weak_learner
        del self.n_elements
        del self.learning_rate
        del self.f
        del self.residuals

Here we see the class defined, along with its initialiser and destructor functions:

__init__(self,weak_learner,n_elements,learning_rate) : this private function initialises the class instance and takes in as arguments the weak learner model (weak_learner), and the hyperparameters specifying the number of elements (n_elements) in the ensemble as well as the learning rate (learning_rate).
__del__(self) : this private function cleans up resources allocated to the class instance when the object is deleted.

    #public function to return model parameters
    def get_params(self, deep : bool = False) -> Dict:
        return {'weak_learner':self.weak_learner,'n_elements':self.n_elements,'learning_rate':self.learning_rate}
    
    #public function to train the ensemble
    def fit(self, X_train : np.array, y_train : np.array) -> None:
        #initialize residuals
        r = np.copy(y_train).astype(float)
        #loop through the specified number of iterations in the ensemble
        for _ in range(self.n_elements):
            #make a copy of the weak learner
            model = clone(self.weak_learner)
            #fit the weak learner on the current dataset
            model.fit(X_train,r)
            #update the residuals
            r -= self.learning_rate*model.predict(X_train)
            #append resulting model
            self.f.append(model)
            #append current mean residual
            self.residuals.append(np.mean(r))

get_params(self,deep) : this is a public function to return the input arguments when an object instance is created (this is necessary for using BoostingRegressor instances in scikit-learn functions).
fit(self,X_train,y_train) : this is a public function used to train the ensemble on the set of training predictors (X_train) and associated labels (y_train). The code here carries out the logic defined in the 3-step process at the end of the previous section.

    #public function to return residuals
    def get_residuals(self) -> List:
        return(self.residuals)
    
    #public function to generate predictions
    def predict(self, X_test : np.array) -> np.array:
        #initialize output
        y_pred = np.zeros((X_test.shape[0]))
        #traverse ensemble to generate predictions
        for model in self.f:
            y_pred += self.learning_rate*model.predict(X_test)
        #return predictions
        return(y_pred)

get_residuals(self) : this public function returns a list of the residuals $\bold{r}$ mentioned in the derivation section.
predict(self,X_test) : a public function to produce predictions from the trained ensemble model, using the set of predictors X_test.

Model Analysis

Now that we have an implementation of our algorithm, let’s test it out. To achieve this, I will use the Boston House Prices dataset. As I have already investigated these data in the article on Random Forest, I will not repeat that work here.

To start, let’s load in these data:

## load regression dataset ##
data = load_boston()
X    = data.data
y    = data.target

We can also specify the weak learner to be used here, which will be a regression decision stump:

## initialize a weak learner ##
weak_m = DecisionTreeRegressor(max_depth=1)

And finally, we can define the set of learning rates that we will use:

## set the learning rates to try ##
learning_rates = [0.1,0.01,0.001,0.0001]

Investigate Residuals

I now want to check that the residuals converge as more weak learners are added to the ensemble. For this investigation, I will fix $n=1000$ :

## loop through the learning rates, record residuals ##
dfRes = pd.DataFrame()
for lr in learning_rates:

    #declare a boosting regressor
    rgr = BoostingRegressor(weak_learner=weak_m, n_elements=1000, learning_rate=lr)
    
    #fit the model
    rgr.fit(X,y)
    
    #record residuals
    dfRes[str(lr)] = rgr.get_residuals()

The residuals for each learning rate are stored in the pandas dataframe dfRes. We can now easily visualise the results:

## plot the residuals ##
dfRes.plot()
plt.title('Residuals by Number of Component Trees in Boosting Ensemble')
plt.xlabel('Number of Component Trees')
plt.ylabel('Mean Residual')
plt.show()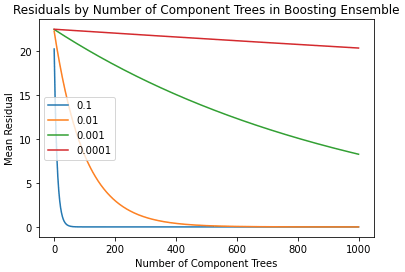

It’s clear to see that the residuals do tend towards zero as the number of elements in the ensemble is increased. It is also apparent that the speed of this convergence is strongly dependent on the learning rate.

Investigate Performance

Here we will use 10-fold cross validation to measure the performance of our boosting regressor. We will repeat this analysis for each of the 4 learning rates defined earlier. Let’s set the number of weak learners in the ensemble to 1000:

## define the scoring metrics ##
scoring_metrics = {'mae': make_scorer(mean_absolute_error), 
                   'mse': make_scorer(mean_squared_error),
                   'r2': make_scorer(r2_score)}
                   
## loop through each learning rate & evaluate for n_elements=1000 ##
for lr in learning_rates:
    #define the model
    rgr = BoostingRegressor(weak_learner=weak_m, n_elements=1000, learning_rate=lr)
    #cross validate
    dcScores = cross_validate(rgr,X,y,cv=10,scoring=scoring_metrics)
    #report results
    print('Learning Rate: ',lr)
    print('Mean MAE: %.2f' % np.mean(dcScores['test_mae']))
    print('Mean MSE: %.2f' % np.mean(dcScores['test_mse']))
    print('Mean R2: %.2f' % np.mean(dcScores['test_r2']))
    print('')

Learning Rate: 0.1

Mean MAE: 3.02

Mean MSE: 20.08

Mean R2: 0.48

Learning Rate: 0.01

Mean MAE: 3.16

Mean MSE: 21.63

Mean R2: 0.52

Learning Rate: 0.001

Mean MAE: 8.75

Mean MSE: 116.08

Mean R2: -1.79

Learning Rate: 0.0001

Mean MAE: 20.31

Mean MSE: 491.88

Mean R2: -14.08

I also re-ran the above code for an ensemble of 10000. The results of both runs are summarised below:

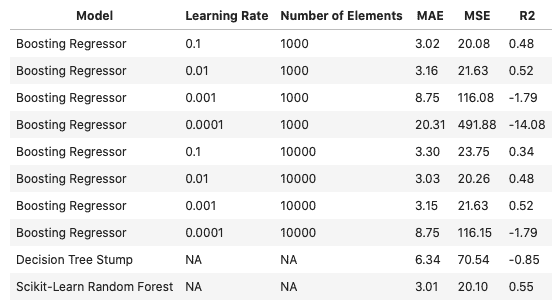
Note that the performance of a lone regression decision stump, as well as a Random Forest, are included.

The best overall boosting regressor was the one with the largest learning rate ( $\alpha=0.1$ ) and smallest number of elements ( $n=1000$ ). This simple boosting model performed to a similar level as the scikit-learn random forest on these data. As a point of comparison, note that the lone decision tree stump was significantly less effective. This illustrates the power of boosting.

Something curious happens when the number of elements is increased to $n=10000$ . The model with $\alpha=0.1$ shows a decrease in performance with respect to its $n=1000$ counterpart. Instead, a smaller learning rate ( $\alpha=0.01$ ) now shows optimal results. What has happened is that the ( $n=10000$ , $\alpha=0.1$ ) model has overfit the data. The increased number of weak learners, in the ensemble, requires a smaller learning rate to optimally fit the data ( $\alpha=0.01$ ). Even smaller learning rates ( $\alpha<0.01$ ) also show poor performance, due to underfitting. Generally speaking, the learning rate $\alpha$ and number of weak learners $n$ , need to be balanced to achieve good results.

Final Remarks

In this post we covered an introduction to simple boosting regression in Python. The key components to this article includes:

The motivation and background for boosting ensembles
The algorithm for a basic boosting regression ensemble
How to implement the algorithm for simple boosting regression in Python
The importance of the learning rate ( $\alpha$ ) – number of weak learner ( $n$ ) trade-off

I sincerely hope you enjoyed this article, and learned something from it. Please check out my GitHub page for the code presented here, and in my other articles.

Hi I'm Michael Attard, a Data Scientist with a background in Astrophysics. I enjoy helping others on their journey to learn more about machine learning, and how it can be applied in industry.

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.