With any machine learning project, it is essential to measure the performance of the model. What we need is a metric to quantify the prediction error in a way that is easily understandable to an audience without a strong technical background. For regression problems, the Mean Absolute Error (MAE) is just such a metric.
The mean absolute error is the average difference between the observations (true values) and model output (predictions). The sign of these differences is ignored so that cancellations between positive and negative values do not occur. If we didn’t ignore the sign, the MAE calculated would likely be far lower than the true difference between model and data.
Mathematically, the MAE is expressed as:
MAE = \frac{1}{N}\sum_i^N|y_{i,pred}-y_{i,true}|
where y_{pred} are the predicted values, y_{true} are the observations, and N is the total number of samples considered in the calculation.
I will work though an example here using Python. First let’s load in the required packages:
## imports ##
import numpy as np
from sklearn.metrics import mean_absolute_error
import matplotlib.pyplot as pltWe can now create a toy dataset. For this example, I’ll generate data using a sine curve with noise added:
## define two arrays: x & y ##
x_true = np.linspace(0,4*np.pi,50)
y_true = np.sin(x_true) + np.random.rand(x_true.shape[0])
We can now plot these data:
## plot the data ##
plt.plot(x_true,y_true)
plt.title('Sinusoidal Data with Noise')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Now let’s assume we’ve built a model to predict the y values for every x in our toy dataset. Let’s plot the model output along with our data:
## plot the data & predictions ##
plt.plot(x_true,y_true)
plt.plot(x_true,y_pred)
plt.title('Sinusoidal Data with Noise + Predictions')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['y_true','y_pred'])
plt.show()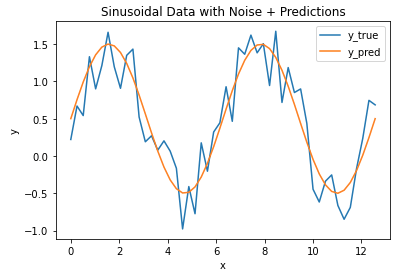
It’s evident that the model follows the general trend in the data, but there are differences. How can we quantify how large the differences are between the model predictions and data? Let’s address this by calculating the MAE, using the function available from scikit-learn:
## compute the mae ##
mae = mean_absolute_error(y_true,y_pred)
print("The mean absolute error is: {:.2f}".format(mae))The mean absolute error is: 0.27
We find that the MAE is 0.27, giving us a measure of how accurate our model is for these data. We can plot these results with error bars superimposed on our model prediction values:
## plot the data & predictions with the mae ##
plt.plot(x_true,y_true)
plt.errorbar(x_true,y_pred,mae)
plt.title('Sinusoidal Data with Noise + Predictions')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['y_true','y_pred'])
plt.show()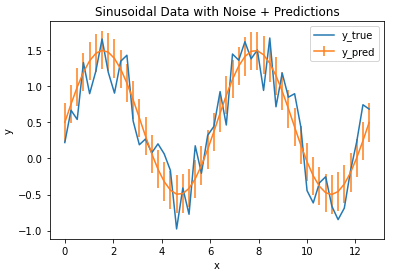
The vertical bars indicate the MAE calculated, and define a zone of uncertainty for our model predictions. We can see that this zone does encompass much of the random fluctuations in our data, and thus provides a reasonable estimate of the model accuracy.
Hi I'm Michael Attard, a Data Scientist with a background in Astrophysics. I enjoy helping others on their journey to learn more about machine learning, and how it can be applied in industry.
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
wow great article
Glad you enjoyed it!
[…] strong resilience to outliers. This is in contrast to other metrics previous discussed, such as the Mean Absolute Error or Mean Squared […]