What is Mini-Batch Gradient Descent? 3 Pros and Cons

Gradient descent is a popular optimisation technique, and forms the basis of many learning algorithms. Perhaps most notably, gradient descent is used when training many types of neural networks. There are a few variants of this technique, but one of the most commonly used is Mini-Batch Gradient Descent. In this post, we’ll introduce this algorithm, and then go over 3 key advantages and disadvantages of this method. Finally, we’ll use 2 illustrative examples in Python to explore some of the aforementioned characteristics of Mini-Batch Gradient Descent. Anyone interested in using this approach, to train their model, should be aware of these points.

Table of Contents

What is Mini-Batch Gradient Descent? 3 Pros and Cons – image by Abi Plata

What is Mini-Batch Gradient Descent?

Generally speaking, gradient descent is an optimisation algorithm that attempts to find the best set of model parameters $\vec{w}$ (otherwise termed ‘weights‘) for a given problem. This is done by first selecting a loss function $\ell$ , by which the effectiveness of the model can be measured. As we improve the values of the weights, the model will perform better on the problem at hand. In other words, as $\vec{w}$ is optimised, $\ell$ will decrease. Therefore, we wish to find the set of model parameters that yields the minimum value of $\ell$ .

Some key points to make note of:

The approach we will take is iterative in nature, meaning we will repeat the stages of our algorithm a number of times as we ‘step’ towards our goal. This will not be an analytical solution.
We need to define a loss function $\ell$ for our problem, that is also a differentiable function of the model parameters $\vec{w}$ . If our problem, or choice of model, does not facilitate this, we cannot use gradient descent.

To move towards the minimum value of $\ell$ , we will compute the derivative with respect to the model parameters, $\partial\ell / \partial w$ . Since the derivative points towards the maximum value of $\ell$ in weight space, we will take a step in the opposite direction. The update rule is therefore defined by:

$\vec{w’} = \vec{w} – \alpha\frac{\partial \ell}{\partial w}$ (1)

where $\vec{w’}$ is the updated set of model parameters after a single step in our algorithm. The learning rate $\alpha$ is a hyperparameter, and controls how large the steps will be. Typical values for $\alpha$ range from 0.1 to 0.001.

We will repeat the update defined in (1) a number of times, until either the magnitude of the update falls below a tolerance threshold $\tau$ , or the maximum number repetitions has been made. At each step, we move towards the loss minimum in weight space. Figure 1 illustrates this scenario:

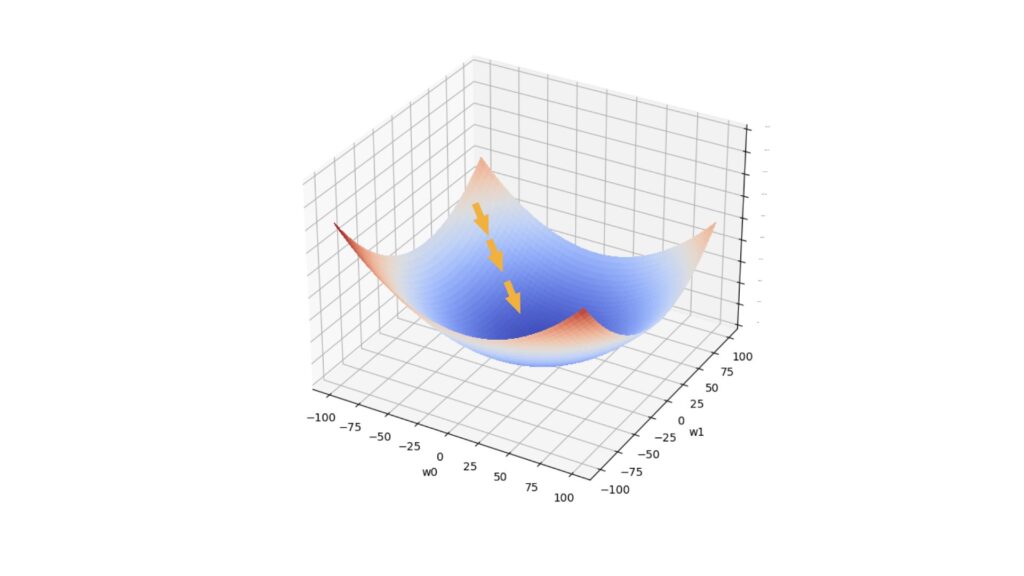
Figure 1: One possible path taken with the gradient descent algorithm. The horizontal axes represent 2 model parameters, whereas the vertical axis represents the loss value. The arrows indicate the movement taken during gradient descent, from a location of high loss to one with low loss.

With Mini-Batch Gradient Descent, we use a subset of the available training data to compute the model parameter updates, at each iteration. These subsets are termed mini-batches, or just batches for short. The total number of batches to use needs to be defined ahead of time, as an additional hyperparameter. Mini-Batch Gradient Descent can be seen as a compromise between Batch Gradient Descent and Stochastic Gradient Descent.

This algorithm consists of the following steps:

Choose values for the learning rate $\alpha$ , tolerance threshold $\tau$ , number of batches, and number of epochs. The latter defines the maximum number of steps we will take in our procedure.
Initialise the values of the model parameters $\vec{w}$ .
for i = 1…\text{number of epochs}:
- randomly shuffle the training data
- for j = 1…\text{number of batches}:
  - select the $j$ ^th batch of training data
  - compute the average derivative $\partial\ell / \partial w$ over the current batch of training data.
  - update the model parameters according to equation (1).
  - check if the magnitude of our update, $\alpha\frac{\partial \ell}{\partial w}$ , falls below $\tau$ . If so, exit the loop.

3 Pros of Mini-Batch Gradient Descent

There are a number of advantages to choosing Mini-Batch Gradient Descent, over other optimisation methods. Let’s outline 3 of the most important here.

I) Provides Greater Accuacy than Stochastic Gradient Descent

In a previous article, I described the Stochastic Gradient Descent algorithm, and provided examples of its use. As its namesake suggests, this is a stochastic process that trades-off accuracy for a lighter computational load. Depending on the size of the learning rate $\alpha$ , this algorithm can also oscillate around a minimum without reaching it.

With Mini-Batch Gradient Descent, the data within each batch is used to compute an average gradient value. This has the effect of “smoothing-out” the path traversed in weight space, thereby minimising the chances of oscillations. This feature can therefore lead to more accurate results, while maintaining a light computational load.

II) Able to Handle Larger Datasets

Since we only concern ourselves with 1 subset of data at a time, it is not required to load all available training data into memory. All that is needed is to have sufficient capacity to handle a single batch of training data, at any given time. As such, we can apply Mini-Batch Gradient Descent to learning problems that involve very large datasets. This contrasts with Batch Gradient Descent, where all the training data needs to be loaded into memory.

III) Able to Escape Local Minima

Although the steps taken with this algorithm are averaged over a batch, there will remain a random component to the path traversed in weight space. The magnitude of this random component will depend on the size of the batch (“batch size” refers to the number of data samples in the batch). Larger batches will have less random movement, whereas smaller batches will have more. As such, it is still possible for this algorithm to escape shallow local minima. This capability will depend on the aforementioned batch size, as well as the learning rate $\alpha$ .

3 Cons of Mini-Batch Gradient Descent

There are also some downsides to using Mini-Batch Gradient Descent in a given machine learning project. Let’s outline 3 of the most relevant.

I) More Complex Algorithm

In contrast to other gradient descent variants, Mini-Batch Gradient Descent is a more complex algorithm. This in-turn implies a more complex implementation into code. More complexity increases the chances of something going wrong in our solution, as well as hurting explainability.

II) Additional Hyperparameter

Related to the previous point; an additional hyperparameter, in the form of the number of batches, needs to be set before Mini-Batch Gradient Descent can be used. This increases the burden of hyperparameter tuning a model we are attempting to train.

III) Less Accurate than Batch Gradient Descent

Only a random subset of the training data is used when calculating the weight updates, on any given iteration. As such, the path traversed in weight space will have a random component, which can prevent the algorithm from “zeroing-in” on the minimum. This contrasts with Batch Gradient Descent, where all the training data is used to determine the weight updates at each iteration.

Python Examples

I would now like to make some of the concepts discussed more tangible. Let’s work through an implementation of Mini-Batch Gradient Descent in Python, and test it with two different functions on a simple toy dataset. As a model to train, we will be making use of a simple linear regression.

MSE Loss Function

The mean squared error (MSE) is a common loss function used in regression problems. This is due to its simplicity, as well as to the fact that it is differentiable. Mathematically this is given by:

$\ell = \frac{1}{2N}\sum^N_i (y_{i,pred}-y_{i,true})^2$ (2)

where $y_{i,true}$ are the true target values, and $y_{i,pred}$ are the model predictions. For our purposes here, the latter quantity is given by: $y_{i,pred} = w_0 + w_1x_i$ , where $w_0$ is the bias, $x_i$ is a single predictor feature, and $w_1$ is the corresponding weight for this feature. Note that $\ell$ is a convex function of the model parameters. Figure 2 visualises this function below.

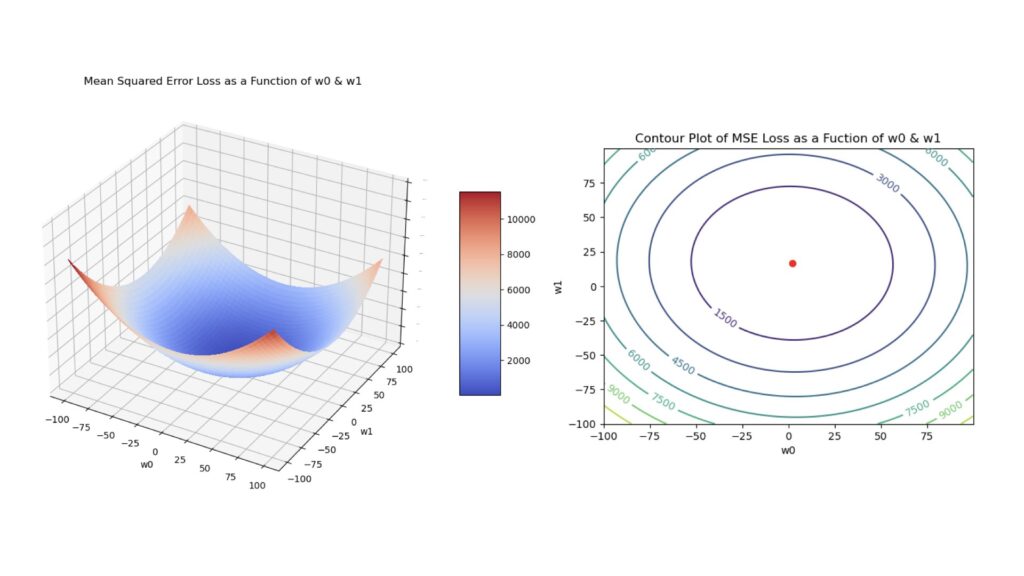
Figure 2: Surface plot (left) and contour plot (right) of the MSE loss. These plots were generated using a simple linear regression to produce predictions, and each plot was made as a function of the model parameters $\vec{w} = [w_0, w_1]$ . The red dot in the contour plot indicates the location of the global minimum.

Trigonometric Function

Let’s also define a more complicated function, that will produce a surface with many local minima and maxima. This function is defined by:

$\ell = \frac{1}{2N}\sum^N_i \theta_i^2sin\left(\frac{\pi \theta_i}{50}\right)$ (3)

where $\theta_i = (y_{i,pred}-y_{i,true})$ , and all the other parameters are the same as was defined for the MSE loss. Note that in this case, $\ell$ is non-convex. Figure 3 illustrates this function below:

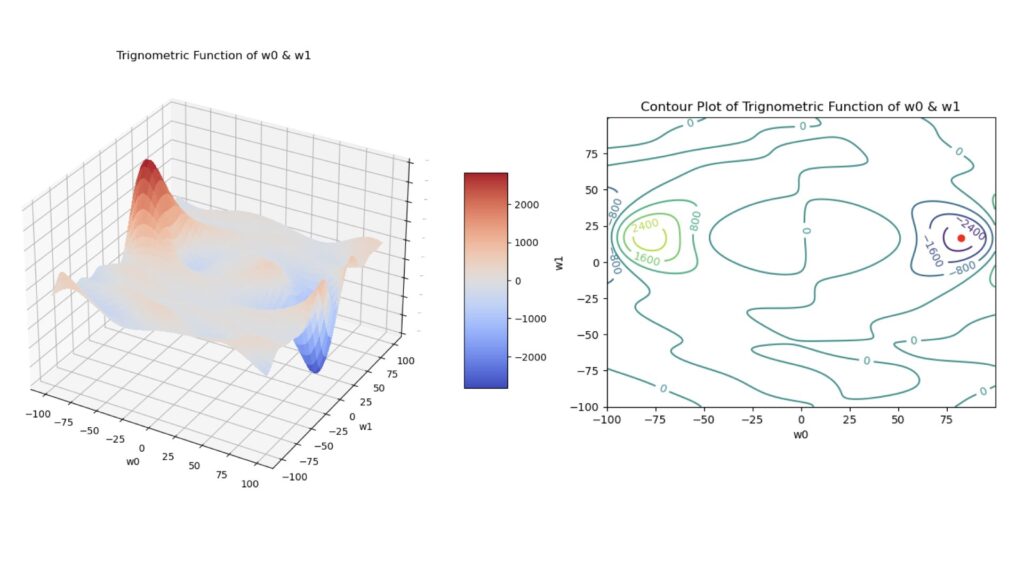
Figure 3: Surface plot (left) and contour plot (right) of the trigonometric function defined in (3). These plots were generated using a simple linear regression to produce predictions, and each plot was made as a function of the model parameters $\vec{w} = [w_0, w_1]$ . The red dot in the contour plot indicates the location of the global minimum.

Note that (3) is not a loss function used in machine learning, as the minimum of $\ell$ does not coincide with our desired state (i.e. $y_{i,pred}=y_{i,true}$ ). We will make use of it here simply because it provides a highly complex surface, with local maxima and minima, in weight space.

Implement Mini-Batch Gradient Descent

We can now put together a single Python function that will encompass the Mini-Batch Gradient Descent algorithm. This code will make use of the numpy package.

# imports
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
from typing import Callable, Tuple, Union
from sklearn.datasets import make_regression
from sklearn.metrics import mean_squared_error, mean_absolute_error

def mini_batch_gradient_descent(X: np.array, 
                                y: np.array, 
                                model: Callable, 
                                Dloss: Callable, 
                                n_batches: int=10,
                                lr: float=0.1, 
                                epochs: int=500,
                                tol: float=1e-4,
                                verbose: bool=False) -> Tuple[np.array, list]:
    """
    Function to compute mini-batch gradient descent for the provided training data using the input model & loss
    
    Inputs:
        Inputs:
        X         -> predictor values
        y         -> true target values
        model     -> function to compute model predictions
        Dloss     -> function to compute the derivate of the loss function in weight space
        n_batches -> number of batches to partition the training data
        lr        -> learning rate
        epochs    -> number of epochs to train
        tol       -> tolerance for early stopping
        verbose   -> boolean to determine if extra information is printed out
        
    Output
        tuple containing a numpy array with the obtimised weights & list of the traversed path in weight space
    """
    # initialise weights 
    w_max  = 100.0
    w      = w_max*(np.random.rand(X.shape[1],1) - 0.5)
    w_path = []
    
    # cycle through epochs and update weights using batch gradient descent
    for _ in range(epochs):
        # shuffle data
        idx = np.random.permutation(X.shape[0])
        X   = X[idx,:]
        y   = y[idx].reshape(-1,1)
        # cycle through each batch of training data
        batch_size = int(X.shape[0]/n_batches)
        for i in range(n_batches):
            # set bounds for the current batch & partition data
            start = i*batch_size
            stop  = start + batch_size
            if i < (n_batches-1):
                X_batch = np.copy(X[start:stop,:])
                y_batch = np.copy(y[start:stop])
            else:
                X_batch = np.copy(X[start:,:])
                y_batch = np.copy(y[start:])
            # store current weight values
            w_path.append(w.tolist())
            # make predictions
            yp = model(X_batch,w)
            # compute the weights update & check tolerance
            dw = lr*Dloss(X_batch,y_batch,yp)
            w -= dw
            w = np.where(w > 100, 100, w)
            w = np.where(w < -100, -100, w)
            if np.linalg.norm(dw) < tol:
                break
            
    if verbose:
        yp = model(X,w)
        print(f"Error metrics: MSE = {mean_squared_error(y,yp):.2f}, MAE = {mean_absolute_error(y,yp):.2f}")
        print(f"Final weights: {float(w[0]):.2f}, {float(w[1]):.2f}")
    
    return (w, w_path)

The training data is composed of an array of predictor features X, and associated true target values y.
The input argument model is a function used to compute predictions at each iteration of the algorithm.
Dloss is another function, that computes the derivative of the (loss) function we are using.
n_batches yields the number of batches we will partition the training data into.
The learning rate lr was termed $\alpha$ in (1). This controls the magnitude of the update step at each iteration.
The epochs argument defines the maximum number of times we pass through the entire set of training data. This is also the same as the number of iterations in our algorithm.
The tolerance tol, referred to as $\tau$ above, sets a lower bound for the size of our updates. The algorithm stops early if the magnitude of the update falls below this value.
The boolean argument verbose controls if performance metrics, and the final weights, are printed out once the algorithm finishes.

Let’s now write the remaining functions we’ll need for our tests. This will include a function for generating predictions from a linear regression model, as well as calculating the derivatives of (2) and (3):

def model(X: np.array, w: np.array) -> np.array:
    """
    Function to compute a linear model
    
    Inputs:
        X -> predictor values
        w -> weights
        
    Output:
        numpy array of predicted target values
    """
    return np.matmul(X,w)
    
def mse_gradient(X: np.array, y: np.array, yp: np.array) -> np.array:
    """
    Function to compute the derivative of the mse loss
    
    Inputs:
        X  -> predictor values
        y  -> true target values
        yp -> predicted target values
        
    Output
        numpy array containing the mse gradient
    """
    return 1/(X.shape[0])*np.sum(X*(yp-y).reshape(-1,1),axis=0).reshape(-1,1)
    
def trig_gradient(X: np.array, y: np.array, yp: np.array) -> np.array:
    """
    Function to compute the derivative of the trignometric function
    
    Inputs:
        X  -> predictor values
        y  -> true target values
        yp -> predicted target values
        
    Output
        numpy array containing the trignometric gradient
    """
    theta = yp - y
    return 1/(X.shape[0])*np.sum((theta*X)*(2*np.sin(np.pi*theta/50)
                                            +(np.pi*theta/50)*np.cos(np.pi*theta/50)),axis=0).reshape(-1,1)

Create a Toy Dataset

I will make use of the make_regression function, from scikit-learn, to produce some data:

# make a simple regression dataset
X, y, coef = make_regression(n_samples=1000, n_features=1, noise=5, bias=2, coef=True, random_state=42)

Let’s visualise the data we’ve just created:

# plot the generated data
plt.scatter(X,y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Generated Dataset')
plt.show()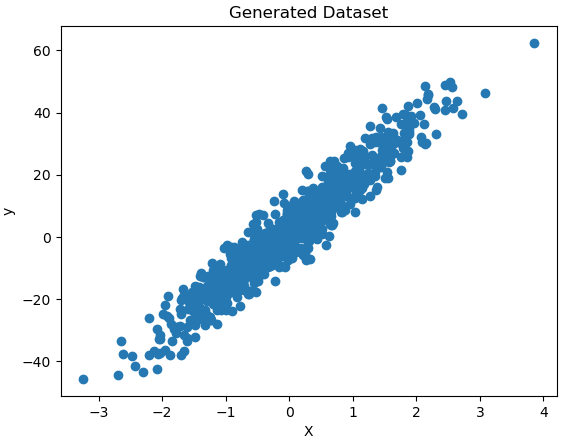

Figure 4: Generated toy dataset

Before testing our implementation on these data, let’s first add a column of 1’s to X to account for the bias parameter $w_0$ . Afterwards, we can also make note of the true value of $w_1$ :

# add bias term
b = np.ones((X.shape[0],1))
X = np.concatenate((b,X),axis=1)

# reshape true labels
y = y.reshape(-1,1)

# what is the model parameter?
coef

array(16.74825823)

Note that the true value of $w_0$ was set to 2.0 when we made the call to make_regression (see the bias input argument).

Mini-Batch Gradient Descent with MSE Loss

We can now test out our implementation using the MSE loss function, with 100 epochs, 20 batches, and verbose set to True. All other parameters are set to their default values:

w, w_path = mini_batch_gradient_descent(X, y, model, mse_gradient, n_batches=20, epochs=100, verbose=True)

Error metrics: MSE = 24.53, MAE = 3.95
Final weights: 1.94, 16.82

The final weight values look quite good! Indeed they are very close to the true values of (2.0, 16.75).

I ran this code 3 separate times, to record the paths traversed by our implementation. Let’s take a look at how those trials turned out:

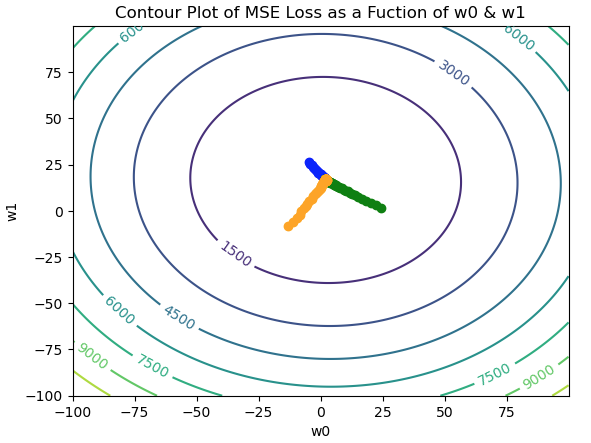
Figure 5: Contour plot for the MSE loss function, with 3 separate paths traversed in weight space. The paths are indicated in blue, green, and orange, and all converge to the global minimum near the center of the figure.

It is apparent in Figure 5 that each trial converges to the same point, regardless of the initial ( $w_0,w_1$ ) position. Note that the paths are smoother that what was observed with Stochastic Gradient Descent. Nevertheless, some random oscillations are still visible in the trajectories.

Mini-Batch Gradient Descent with Trigonometric Function

Let’s now test out our implementation using the trigonometric function, described in equation (3). Here I’ll set the learning rate $\alpha$ to 0.01, the number of batches to 20, and request 1000 epochs:

w, w_path = mini_batch_gradient_descent(X, y, model, trig_gradient, n_batches=20, 
                                        lr=0.01, epochs=1000, verbose=True)

Error metrics: MSE = 6426.70, MAE = 80.01
Final weights: 82.02, 17.20

We can see the resulting weights are not nearly as close to the true values, as was seen previously. Unsurprisingly, the quality of the final generated predictions, reflected through the reported error metrics, is also not as good.

Like before, I ran this experiment 3 times and recorded the paths traversed in weight space. Let’s look at these results:

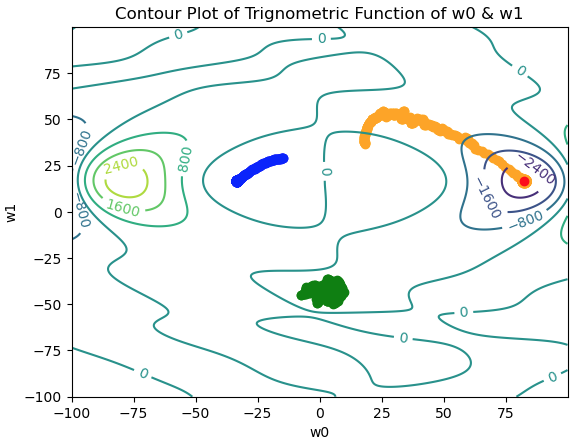
Figure 6: Contour plot for the trigonometric function described in (3), with 3 separate paths traversed in weight space. The paths are indicated in blue, green, and orange. Note the lack of convergence; there is no single point all the paths converge to. The true global minimum is indicated in red.

We can see the 3 trials move towards minima within their vicinity, however the positions settled upon are highly dependent on the initial starting positions in weight space. Two out of three trials (blue & green) find two different local minima in weight space. The orange trial manages to find the global minima. Note each path has a different appearance to its trajectory:

The blue path is smooth from start to finish.
The green path appears to oscillate near it’s starting position, with no clear direction.
Only the orange path has a combination of a clear trend, and random component, to its motion.

The only difference between each trial was the starting position in weight space. As such, the most likely explanation for these observations lies in the different weight-space topologies these trials occurred in.

Final Remarks

In this post we have covered:

What is the Mini-Batch Gradient Descent algorithm, and what it is used for.
3 Pros and Cons for using this variant of gradient descent.
How to implement Mini-Batch Gradient Descent in Python from scratch.
Explored how well does Mini-Batch Gradient Descent do when applied to convex and non-convex functions.

I hope you enjoyed this article, and gained some value from it. If you would like to take a closer look at the code presented here, please take a look at my GitHub. If you have any questions or suggestions, please feel free to add a comment below. Your input is greatly appreciated.

About Author

Hi I'm Michael Attard, a Data Scientist with a background in Astrophysics. I enjoy helping others on their journey to learn more about machine learning, and how it can be applied in industry.

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.