In my previous post, I covered PageRank, an unsupervised graph algorithm made famous as the original basis of the Google search engine. Here we’ll expand on the work done in that previous post, to describe the Weighted PageRank algorithm. We will first cover what the Weighted PageRank algorithm is, before diving into a mathematical description. Next, we will implement this algorithm in Python, and test out the results on a toy dataset. All code presented here can also be downloaded from my Github.
Table of Contents

Implement the Weighted PageRank Algorithm in Python – image by author
What is Weighted PageRank?
PageRank was originally developed at Google by Larry Page and Sergey Brin. This algorithm is best known for being the original basis of the Google Search Engine.
The original intent of PageRank is to figure out how to order webpages from a search result. The key assumption made is: more popular/relevant webpages will tend to have more links to other webpages. More specifically, the most relevant pages will tend to have the largest number of incoming links from other webpages. PageRank therefore assigns a score to each webpage, based on its interconnectivity with other webpages. These scores (or ranks) can be used by a search engine to sort the resulting websites, in order of most-relevant to least.
In its original form, PageRank treats each link between webpages as equally important. With Weighted PageRank, this simplification is dropped. Instead, weights are calculated that specify the importance of a connection. These weights can be computed based on any attribute of the dataset, and will ultimately depend on the nature of your problem. Within the context of webpages on the internet, these weights can be computed based upon the number of incoming and outgoing links from a particular page.
Fundamentally, PageRank can be categorized as a Graph Algorithm, since the relation of webpages on the internet can be modeled as a directed graph. In this way, the nodes in the graph represent webpages, and edges indicate links between said pages. Let’s take a peek at a small example:
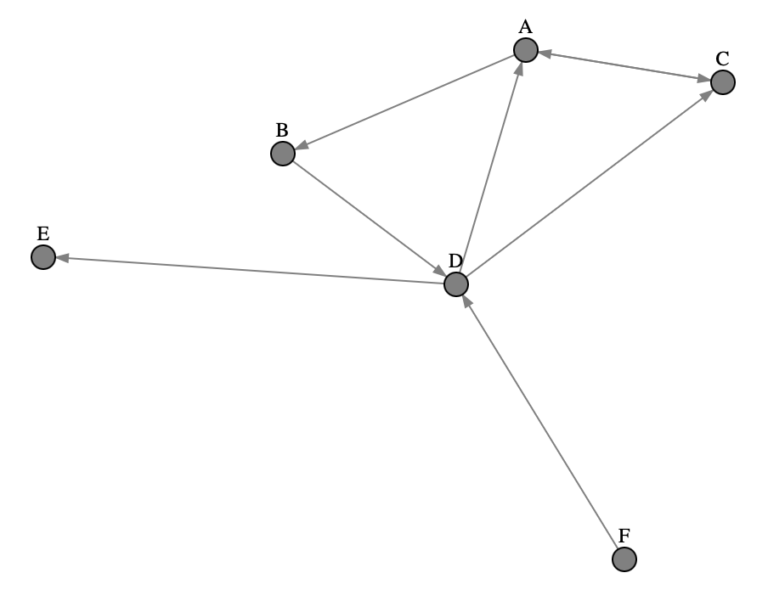
Figure 1: Illustration of a simple directed graph consisting of 6 nodes.
The illustration above shows the relations between 6 different webpages: A, B, C, D, E, and F. Taking a quick look at Figure 1, we can see that nodes A and D have the largest number of incoming and outgoing links. As such, we shouldn’t be too surprised if these nodes end up receiving the highest rank values. Conversely nodes E and F have just single incoming and outgoing links, respectively, which should result in low rank values. Let’s come back to these guesses once we test out this algorithm in the next sections!
It is important to note that although PageRank was originally developed for the task of web search, it is not limited to this. The PageRank algorithm can be applied to any problem that can be modeled as a graph, where the relevance/ranking of nodes is useful to know.
The Weighted PageRank Algorithm
We saw in the previous post the update rule for PageRank over iteration t=0,1,2,…:
{\bf P_r(t+1)} = d{\bf \hat{O}P_r(t)} + \frac{1-d}{N_p}{\bf 1}
where:
- d is the damping factor
- N_p is the number of nodes (i.e. webpages) in the graph
- {\bf P_r(t)} is a column vector containing all the page ranks at step t
- {\bf \hat{O}} is a modified form of the adjacency matrix, where each element \hat{O}_{i,j} is the ratio of edges from j \rightarrow i divided by the total out-degree of node j
- {\bf 1} is a column vector consisting of N_p elements all set to 1.0
We can continue updating until convergence is reached as set by a tolerance parameter \epsilon:
|{\bf P_r(t+1)} – {\bf P_r(t)}| < \epsilon
For Weighted PageRank, we replace {\bf \hat{O}} with a weights matrix {\bf W} in our update rule such that:
{\bf P_r(t+1)} = d{\bf WP_r(t)} + \frac{1-d}{N_p}{\bf 1} (1)
and:
{\bf W} = \begin{bmatrix} w_{0,0} && w_{0,1} && \cdots && w_{0,N_p} \\ w_{1,0} && w_{1,1} && && \vdots \\ \vdots && && \ddots && \\ w_{N_p,0} && \cdots && && w_{N_p,N_p} \end{bmatrix} (2)
where each element w_{i,j} is the weight for the edge connecting nodes j \rightarrow i, and can take on a value between [0.0,1.0].
Technically, {\bf W} can be computed any way in which you desire to weight the edges. The choice for how you determine the weights will depend on the problem you’re working on.
For the specific case of web pages, we can determine each element of {\bf W} by first computing:
w_{i,j} = w^{in}_{j \rightarrow i} \times w^{out}_{j \rightarrow i} (3)
where:
w^{in}_{j \rightarrow i} = \frac{\textrm{number of incoming edges for} \: i}{\textrm{sum of all incoming edges for all nodes that link with} \: j} (4)
w^{out}_{j \rightarrow i} = \frac{\textrm{number of outgoing edges for} \: i}{\textrm{sum of all outgoing edges for all nodes that link with} \: j} (5)
After computing each of these elements we can normalize the weights, with respect to all the outgoing edges from node j, to arrive at matrix {\bf W}.
Implement Weighted PageRank into Code
Let’s now proceed to implement the algorithm, covered above, into Python code. We will have a sole dependency to import:
import numpy as npTo avoid duplicate effort, we can run the notebook used in my original PageRank post, to import all the objects we created at that time:
%run Notebook\ XXIX\ Learn\ the\ PageRank\ Algorithm\ with\ 1\ Simple\ Example.ipynbRunning the above line of code will bring in the Graph and PageRank classes built for the classic PageRank. Our implementation here involves writing subclasses that will inherit the logic from these two classes:
class WeightedGraph(Graph):
def _build_weight_matrix(self) -> np.array:
W = np.zeros((len(self.nodes),len(self.nodes)))
edges = np.array(self.edges)
for node in self.nodes:
# get all outgoing link nodes from node
out_nodes = np.unique(edges[edges[:,0] == node][:,1])
# get counts of incoming and outgoing links for all out_nodes
I = np.array(list(map(self.indegrees.get, out_nodes)))
I[I == None] = 0
O = np.array(list(map(self.outdegrees.get, out_nodes)))
O[O == None] = 0
# compute weight components
w_in = I/np.sum(I)
w_out = O/np.sum(O)
# fill in weights matrix
col_idx = [self.nodes.index(node) for node in out_nodes]
W[self.nodes.index(node),col_idx] = w_in*w_out
return W
def get_weighted_adjacency_matrix(self) -> np.array:
# get the raw weight matrix
W = self._build_weight_matrix()
# normalize weights & return
denominator = np.sum(W,axis=1)
denominator = np.where(denominator == 0, 1., denominator)
return (W.T/denominator)The class WeightedGraph adds two member functions on top of Graph:
- _build_weight_matrix(self) : this protected function computes the raw weights matrix (2) according to equations (3), (4), and (5).
- get_weighted_adjacency_matrix(self) : this public function returns {\bf W} with normalized weights, and properly formatted to have the same form as a adjacency matrix.
class WeightedPageRank(PageRank):
def _step(self, P1: np.array, I: np.array, graph: Graph) -> np.array:
P2 = (
self.damping_factor*np.matmul(graph.get_weighted_adjacency_matrix(),P1)
+ (1 - self.damping_factor)*I/graph.get_number_nodes()
)
return(P2/np.sum(P2))The class WeightedPageRank overwrites the protected _step(self, P1, I, graph) function, to compute the update rule defined by (1).
Run the Weighted PageRank
Here let’s test out the classes we just implemented, to see if the results make sense:
# create a graph object
graph = WeightedGraph(edges)
graph.get_weighted_adjacency_matrix()array([[0. , 0. , 1. , 0.66666667, 0. , 0. ],
[0.33333333, 0. , 0. , 0. , 0. ,0. ],
[0.66666667, 0. , 0. , 0.33333333, 0. ,0. ],
[0. , 1. , 0. , 0. , 0. ,1. ],
[0. , 0. , 0. , 0. , 0. ,0. ],
[0. , 0. , 0. , 0. , 0. ,0. ]]) Each column shows the fraction of the page rank that is distributed to other nodes at each iteration . For example, the first column shows how the page rank of node A is distributed: 33.3% goes to node B, while 66.7% goes to node C.
# create a pagerank object
pr = WeightedPageRank()
# compute pageranks
ranks = pr.evaluate(graph)
ranks{'A': 0.3681734599108074,
'B': 0.132187163250422,
'C': 0.2859159868057953,
'D': 0.16261318236879824,
'E': 0.025555103832088505,
'F': 0.025555103832088505} We can tabulate the results, in order to compare with the classic PageRank:
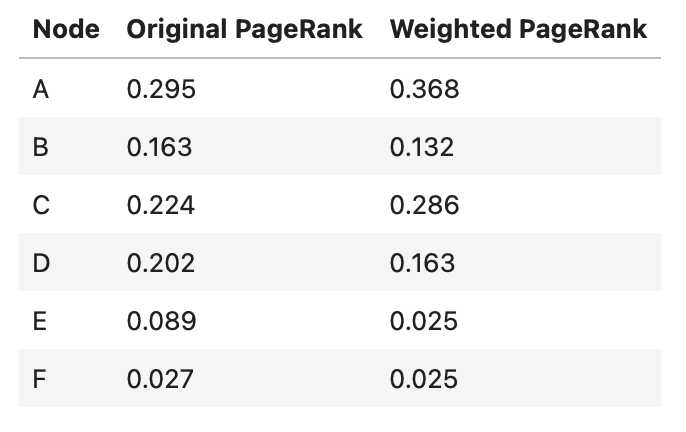
Here we can see how the edge weights affect the ranking results. Some of the most notable changes is the increase in page rank to nodes A and C, whereas nodes B and D see a decrease. Node D is peculiar, in that it is linked to a dangling node (E). I covered dangling nodes in a recent video. The presence of such nodes will certainly affect the results, and as such if we properly treat for E, the rankings for both D and E will likely increase.
Final Remarks
In this post you have learned:
- What Weighted PageRank is, and why this algorithm was developed.
- The mathematics behind the Weighted PageRank algorithm.
- How to implement the Weighted PageRank algorithm into code.
I hope you enjoyed this article, and gained some value from it. If you would like to take a closer look at the code presented here, please take a look at my GitHub. If you have any questions or suggestions, please feel free to add a comment below. Your input is greatly appreciated.
Note I have started a New Monthly Newsletter! At the end of each month I will send out this free newsletter to each of my subscribers by email. This is the best way to stay on top of my latest content. Sign up for the newsletter here!
Related Posts
Hi I'm Michael Attard, a Data Scientist with a background in Astrophysics. I enjoy helping others on their journey to learn more about machine learning, and how it can be applied in industry.

Hey Michael 👋 Thank you for instructional piece! I wonder; which use cases can you imagine for the weighted PageRank algorithm?
Hi Lubo! Thanks for the kind words. Regarding your question, there are various possible applications for Weighted PageRank:
* The ranking of webpages on the internet, where links are weighted according to how they are connected on the web. This is the example I work through in the post.
* Investigating financial crime, where the graph is built using transaction data. In this scenario, the edges represent transactions between different business parties/financial institutions. The edges can be weighted according to some aspect of these transactions (monetary amount, frequency of transactions, etc).
* Infectious disease propagation. In this case, the graph can be composed of nodes that represent individuals, and the edges represent interactions between individuals. The edges can be weighted based upon how likely the interactions are to transmitting the disease.
* Measure the impact of scientific researchers. In this case, the graph would be composed of nodes representing the individual researchers, and the edges represent when their work is cited by other authors. The edges can be weighted by how often their work gets cited.
Keep in mind there are many other possible applications, I’ve just listed here what came to mind 🙂